基于模板匹配的视频马赛克实时检测
本方法来自于论文《Fast Mosaic Detection for Real-time Video Based on Template Matching Strategy》。
算法描述
- 计算图像的灰度梯度 使用Canny边缘检测算子(论文阐述的是Canny算子,但Canny检测是基于Sobel算子的多步骤检测,因此在实现时采用Sobel算子),分别计算得到水平方向和竖直方向的灰度梯度,称为灰度一阶导数。Sobel算子如下图所示,\(G_x\)是用于计算水平梯度,\(G_y\)用于计算竖直梯度。(文末附有梯度计算原理)
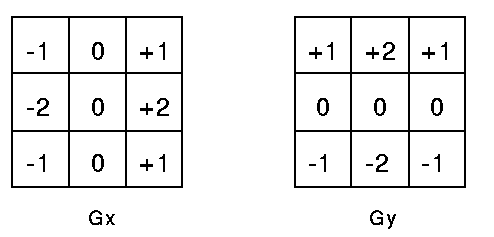 根据计算原理可知,\(G_x\)计算得到的在数值上反映了图像在水平方向的突变程度,如果图像上有很多竖条纹,那么其水平梯度将会很高。类似的,\(G_y\)可可以反映图像中横条纹情况。
根据计算原理可知,\(G_x\)计算得到的在数值上反映了图像在水平方向的突变程度,如果图像上有很多竖条纹,那么其水平梯度将会很高。类似的,\(G_y\)可可以反映图像中横条纹情况。 - 得到二值边缘图 选择合适的门限值,让水平和竖直的灰度图二值化。如果灰度值高于门限值为255,低于门限值设为0。 门限的选择很关键:门限越低,边缘线越多,检测结果越容易受到噪音影响。相反,门限过高,将导致图像细节丢失。
- 预处理边缘图像 计算灰度梯度\(G_x\)在每一列的二值总和,设定一个门限值,如果总和值大于等于线门限,则表明这列存在竖条纹,记下该列位置,如果低于线门限,什么也不做。对水平方向做类似处理,计算\(G_y\)在每行的二值总和,设定门限值,记下可能存在横条纹的行位置。
- 使用模板匹配检测相交位置的Mosaic Point 行列位置相交的点可能是马赛克点,但需要进一步检测判断。在候选点左、右、上和下四个方向,统计二值灰度梯度值为255的点数。如果点数表明,该位置存在下图所示的五个模板之一,则判定该点是马赛克点。
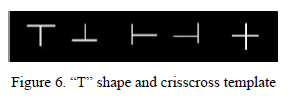
- 识别马赛克图片 设定一定的门限值,如果马赛克点足够多,则可认为是该图存在马赛克。
Canny边缘检测详解
一直对边缘检测算子一知半解,网上的也都是摘抄别人的理论,下面自己写写。
opencv中的canny函数
void Canny(InputArray img, //单通道8位输入图像 OutputArray edges, //输出边缘图,和img有相同size和type double thresh1, //first threshold for the 滞后处理程序 double thresh2, //second threshold for the hysteresis procedure int apertureSize = 3, //孔径 size for the Sobel() operator. bool L2gradient = false);
L2gradient = ture:\(L_2=\sqrt{(\frac{dI}{dx})^2+(\frac{dI}{dy})^2}\)用于计算图像梯度值;
L2gradient = false:\(L_1=|\frac{dI}{dx}|+|\frac{dI}{dy}|\)void cvCanny(const CvArr* image, CvArr* edges, double thresh1, double thresh2, int apertureSize = 3);
以上函数可以帮助我们从一副图像获得包含符合条件的边缘图像edges,需要给定两个门限值。但中间的处理过程不是很清楚。
Canny边缘检测算法
算法处理过程:
- 对输入的灰度图进行Gaussian滤波,除燥; 高斯核尺寸的大小会影响检测结果,尺寸越大,检测器对噪音的敏感程度越低,对局部边缘的检测错误将会稍多。需根据实际情况选择。
- 找到图像中梯度强度; 图像的边可以指向很多方向,所以Canny算法使用四个filter检测横、竖、斜边。边缘检测算子(例如Robets,Prewitt或Sobel)返回的是水平方向、竖直方向的一阶导数值\(G_x\)、\(G_y\)。根据这两个值,可以得出边的幅值G和方向\(\theta\)。\[G=\sqrt{G_x^2+G_y^2}\]\[\theta=atan2(G_y, G_x)\]
- 非极大值抑制法; 非极大值抑制主要用于"瘦边"。梯度计算后,从梯度值提取的边很模糊,对于图像的边,应当只有一个精确响应,因此,本步骤只保留局部最大值,抑制了所有梯度值为0,局部最大值表示了强度变化最尖锐的位置。
- 双门限决定潜在边缘;
- 根据hysteresis跟踪边缘。
附:梯度推导
假设数字图像在(x,y)位置的像素值记为\(f(x,y)\)(注意:以水平方向为x,以竖直方向为y),在该位置的梯度由二维列向量定义:
\[\nabla \vec f=\begin{bmatrix}G_x \\ G_y\end{bmatrix}=\begin{bmatrix}\frac {\partial f} {\partial x} \\ \frac {\partial f} {\partial y}\end{bmatrix}\tag{1}\] 该梯度向量的模值通常被称为“梯度”,可通过下式计算得到:\[\nabla f = |\nabla \vec f| = {\sqrt{ {G_x}^2+{G_y}^2}}\tag{2}\] 为了简化上式梯度值的计算,用如下近似求解梯度模值:\[\nabla f = |G_x| + |G_y|\tag{3}\] 一阶微分的求解,可通过如下求得:\[\frac {\partial f} {\partial x} = f(x+1,y) - f(x,y)\tag{4}\] 所以,梯度模值可通过下式计算得到:\[\nabla f = |f(x+1,y)-f(x,y)| + |f(x,y+1)-f(x,y)|\tag{5}\] 根据上式,sobel算子就是通过近似等于的思想,将梯度计算进行了转化:利用当前点所在的右排减去左排值,同时赋予当前排的位置较高权重,公式表示如下,\[\nabla f = |[f(x+1,y-1)+2f(x+1,y)+f(x+1,y+1)]-[(f(x-1,y-1)+2f(x-1,y)+f(x-1,y+1))]| \\ +|[f(x-1,y+1)+2f(x,y+1)+f(x+1,y+1)]-[f(x-1,y-1)+2f(x,y-1)+f(x+1,y-1)]|\tag{7}\] 上式第一个绝对值项对应的卷积核就是Sobel的G_x算子,第二个绝对值项对应的就是G_y算子。这就是Sobel算子计算梯度的方法。 (注:冈萨雷斯的书中以竖直方向为x方向,与通常习惯有差异,结果也有差异。)